昨日の続き。

と言いつつ、昨日の内容についてはおろかその他もろもろの理解が不十分だったことに気づいたため、そのあたりを復習しつつ読み進めてる。そのため、本題に入る前に大幅に脱線するので注意されたい（自然消滅しないよう頑張ります）。

変分自己符号化器

このあたり、RBM とか GMM と混同してよくわからなくなる…

変分自己符号化器 (variational autoencoder; VAE) は、大雑把に言えば確率的主成分分析 (probablistic PCA) の非線形版であり、主成分分析に対する自己符号化器 (autoencoder; AE) と同じような立ち位置の確率モデルと考えることができる（多分）。

自己符号化器 (autoencoder) ではデータのもつ特徴量を抽出するデータ $x$ から中間層 $z$ への"確定的な"写像を求めることが目的となる。一方 VAE では、潜在変数 $z$ の事後分布 $p(z|x,\theta)$ 、すなわち特徴量への"確率的な"写像を求めることが目的となる。 $z$ は非常に高次元の空間だったり、深層学習よろしく積層的な構造を持っていたりする（積層変分自己符号化器, Ladder variational autoencoder などと呼ばれるらしい）。

事後分布 $p(z|x,\theta)$ は通常直接求めることは困難であるため、変分近似などを適用し近似的に求めた分布 $q(z|x;\phi)$ を用いる。これは（これは？）認識モデル (recognition model) とも呼ばれ、データ $x$ を特徴量 $z$ へと文字通り "encode" する、学習過程で得る重要な確率モデルの一つである。

潜在変数は連続値を取る。これが $z \in \{0,1\}^s$ であればいわゆる制約ボルツマンマシン (RBM) になり、Hinton らが Deep Berief Network で展開した話につながる。

VAE の生成モデルは次のように与えられる。ハイパーパラメータを $\mu = 0$ , $\Sigma = \mathrm{I}$ と仮定される文献が多いが、今回は明示的に表記した。

$z \sim \mathcal{N}(\mu, \Sigma) = p(z)$
$x \sim p(x \mid z, \theta)$

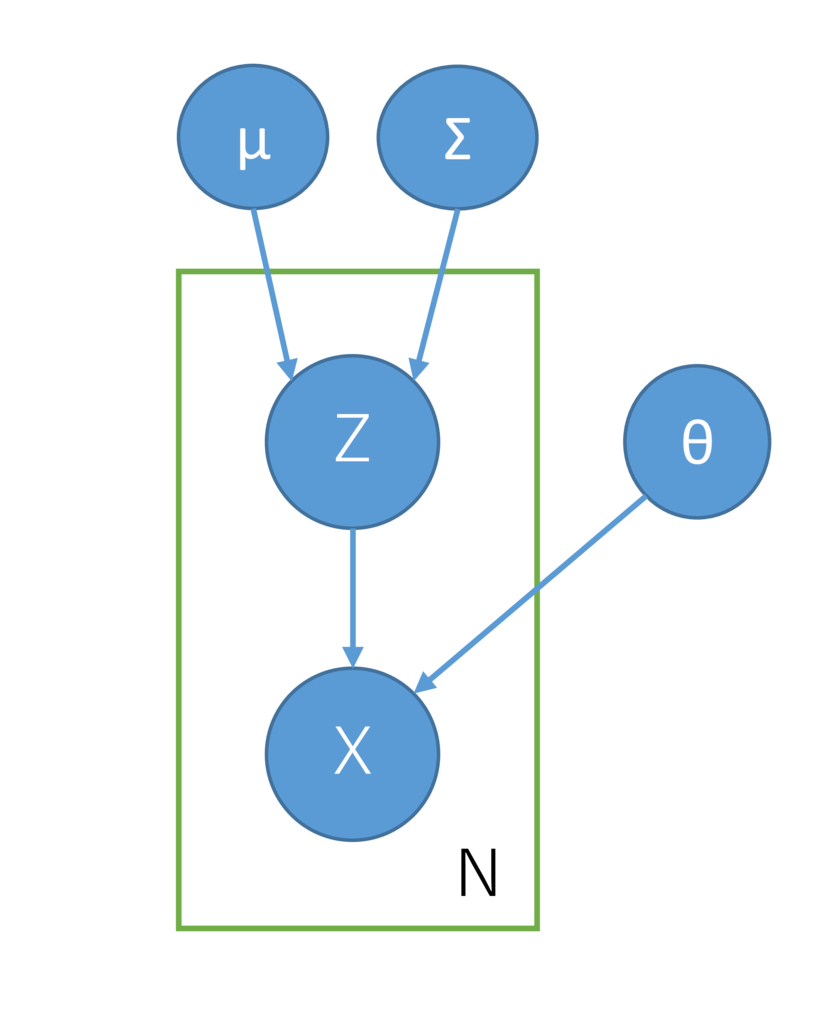
また、グラフィカルモデルは下図のように書くことができる。見た目は GMM に代表される混合モデルそのものであるが、潜在変数が連続値を取る点が異なる。

f:id:ubnt_intrepid:20161012012650p:plain:w250

学習の目標は、対数周辺尤度

$\displaystyle \log p(x) = \log \int_{z} p(z)p(x|z,\theta) dz$

の $\theta$ に関する最大化である。しかし、この値を直接評価するのは困難であるため（Jensen の不等式とか使ってゴニョゴニョして）次に示す変分下限 $\mathcal{L}$ の最大化に置き換える。

$\displaystyle \mathcal{L}(x; \theta, \phi) = \mathbb{E}_{q(z|x,\phi)} \big[ \log p(x|z,\theta) \big] - \mathrm{KL}\big(q(z|x,\phi) \;\|\; p(z|x,\theta)\big)$

ここで $q(z|x,\phi)$ は前述した認識モデルである。上式を $\theta, \phi$ に関し最大化することで認識モデル $q(z|x,\phi)$ および生成モデル $p(x|z,\theta)$ を得る。

問題となるのが、変分下限 $\mathcal{L}$ の勾配計算である。これは $q$ に関する期待値計算が含まれており、解析的な形で容易に求めることができない。そのあたりをうまくやるのが stochastic backpropagation あるいは stochastic gradational variational bayes (SGVB) である。本当はその話をまとめようと思ったけど部屋が寒くなってきたので今日はここまで。

にっき

技術的な話題はないです

深層カルマンフィルタ (2)

変分自己符号化器