…さて、ここからが本題。同じ著者による新しい論文がアップロードされていたので、こちらも適宜参照しながら読み進めていく。

[1609.09869] Structured Inference Networks for Nonlinear State Space Models

問題設定

まずは基本となる状態空間モデルについて説明する。今回対象とする状態空間モデルの生成モデルは次のように記述される。

$z_1 \sim \mathcal{N}(\mu_0; \Sigma_0)$
$z_t \sim \mathcal{N}(G_{\alpha}(z_{t-1}, u_{t-1}, \Delta_t), S_{\beta}(z_{t-1}, u_{t-1}, \Delta_t)) ,\quad t \in \{2,\ldots,T\}$
$x_t \sim \Pi(F_{\kappa}(z_t)) ,\quad t \in \{1,\ldots,T\}$

$x_t \in \mathbb{R}^d, u_t \in \mathbb{R}^c, z_t \in \mathbb{R}^s$ はステップ $t \in \{1,2,\ldots,T\}$ における観測値、外部入力、および潜在状態である。 $\Delta_t$ はステップ $t-1$ から $t$ までの時間幅である。状態遷移確率が直前の状態 $z_{t-1}$ の滞在時間(sojourn time) に依存するため、正確には上のモデルは準マルコフ過程 (semi-Markov process) と呼ばれる確率過程と解釈することもできる。 $G_{\alpha}, S_{\beta}, F_{\kappa}$ は多層パーセプトロンで近似された非線形関数である。

上の生成モデル $p(\mathbf{x}|\mathbf{z},\mathbf{u},\theta)$ のパラメータ $\theta =(\alpha,\beta,\kappa)$ 、および認識モデル $q(\mathbf{z}|\mathbf{x},\mathbf{u}, \phi)$ のパラメータ $\phi$ を求めることが学習の主な目的となる。ただし、 $\mathbf{x} = (x_1, \ldots, x_T)$ , $\mathbf{u}=(u_1,\ldots,u_T)$ 、 $\mathbf{z}=(z_1,\ldots,z_T)$ である。

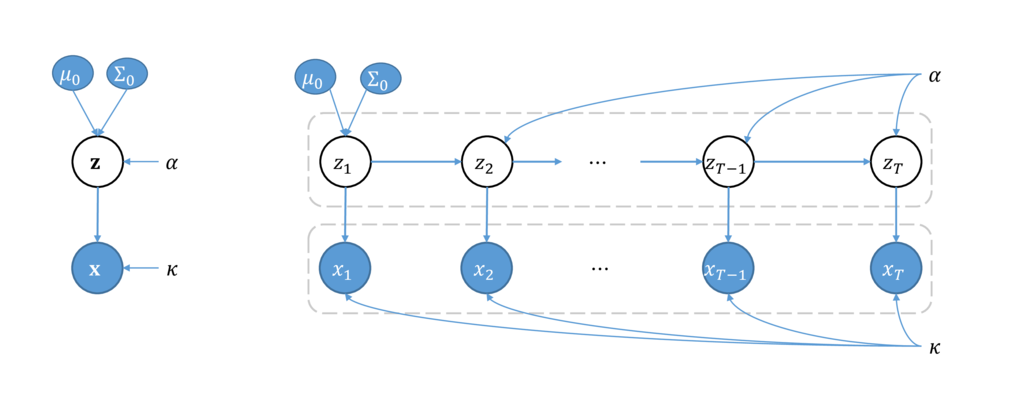
生成モデルのグラフィカルモデルは次のようになる（外部入力は省略）。左側を時間方向に展開すると右図のような形になる。構造としては変分自己符号化器に似ているが、状態遷移確率に関するパラメータも推定の対象になっていること、および状態遷移確率に非線形写像が含まれることから $\mathbf{z}$ の事前分布が正規分布にならない点が異なる。

f:id:ubnt_intrepid:20161014183827p:plain

状態空間モデルの変分下限

さて、上記モデルに対し変分ベイズ学習を考える。まず、マルコフ性より（真の）事後分布は次のように分解することができることに注意する（文献の Theorem 5.1）。

$\displaystyle { p(\mathbf{z}| \mathbf{x}, \mathbf{u}, \phi) = p(z_1|\mathbf{x},\mathbf{u},\phi) \prod_{t=2}^{T} p(z_t | z_{t-1},\; x_t,\ldots,x_T, \; u_{t-1},\ldots,u_{T-1}, \phi) }$

これに対応し、認識モデルを次のように分解する。（上の定理の内容に従うのであれば）すべてのステップにおける外部入力・観測値の値は必要ない気がするけど。

$\displaystyle { q(\mathbf{z}| \mathbf{x}, \mathbf{u}, \phi) = q_1(z_1|\mathbf{x},\mathbf{u},\phi) \prod_{t=2}^{T} q_t(z_t | z_{t-1},\mathbf{x}, \mathbf{u}, \phi) }$

これを用いて、変分下限の各項を整理する（導出はもとの文献などを参照）。まず第一項について整理すると次のようになる。

$\displaystyle { \mathbb{E}_{q(\mathbf{z}|\mathbf{x},\mathbf{u},\theta)}[ \log p(\mathbf{x}|\mathbf{z}, \mathbf{u}, \theta) ] }$

$\displaystyle { = \sum_{t=1}^{T} \mathbb{E}_{q(\mathbf{z}|\mathbf{x},\mathbf{u},\phi)}[\log p(x_t|x_1,\ldots, x_{t-1}, \mathbf{z}, \mathbf{u}, \theta) ] }\quad$

$\displaystyle { = \sum_{t=1}^{T} \mathbb{E}_{q(\mathbf{z}|\mathbf{x},\mathbf{u},\phi)}[\log p(x_t|z_t,\theta) ] }$ 　（グラフ構造より）

$\displaystyle { = \sum_{t=1}^{T} \mathbb{E}_{q(z_t|\mathbf{x},\mathbf{u},\phi)}[\log p(x_t|z_t,\theta) ] }$ 　（ $z_t$ 以外について積分消去）

ただし、 $q(z_t|\mathbf{x},\mathbf{u},\phi) = \sum_{z_1,\ldots,z_{t-1}} q(z_1,\ldots,z_t|\mathbf{x},\mathbf{u},\phi)$ である。この分布は、 $q_t(z_t|z_{t-1}) = q_t(z_t)$ であれば上で分解した認識モデル $q_t$ と一致するが、そうでなければ違う分布となるため、混乱を避けるため別の分布として表記した。

次に第二項のKL情報量は次のようになる。

$\displaystyle { \mathrm{KL}( q(\mathbf{z}|\mathbf{x},\mathbf{u},\phi) \;\|\; p(\mathbf{z}|\mathbf{u},\theta) ) }$

$\displaystyle { = \mathbb{E}_{q(\mathbf{z}|\mathbf{x},\mathbf{u},\phi)}\Big[ \log \frac{q(\mathbf{z}|\mathbf{x},\mathbf{u},\phi)}{p(\mathbf{z}|\mathbf{u},\theta)} \Big] }$

$\displaystyle { = \mathbb{E}_{q(\mathbf{z}|\mathbf{x},\mathbf{u},\phi)}\Big[ \log \frac{q_1(z_1|\mathbf{x},\mathbf{u},\phi)}{p(z_1)} \Big] + \sum_{t=2}^{T} \mathbb{E}_{q(\mathbf{z}|\mathbf{x},\mathbf{u},\phi)}\Big[ \log \frac{q_t(z_t|z_{t-1},\mathbf{x},\mathbf{u},\phi)}{p(z_t|z_{t-1},u_{t-1},\theta)} \Big] }$ 　（被積分項ごとに分解）

$\displaystyle { = \mathbb{E}_{q_1(z_1|\mathbf{x},\mathbf{u},\phi)}\Big[ \log \frac{q_1(z_1|\mathbf{x},\mathbf{u},\phi)}{p(z_1)} \Big] + \sum_{t=2}^{T} \mathbb{E}_{q(z_{t-1}|\mathbf{x},\mathbf{u},\phi)} \Bigg[ \mathbb{E}_{q_t(z_t|z_{t-1},\mathbf{x},\mathbf{u},\phi)} \Big[ \log \frac{q_t(z_t|z_{t-1},\mathbf{x},\mathbf{u},\phi)}{p(z_t|z_{t-1},u_{t-1},\theta)} \Big] \Bigg] }$ 　（積分消去＋整理）

$\displaystyle { = \mathrm{KL}\big( q_1(z_1|\mathbf{x},\mathbf{u},\phi) \;\|\; p(z_1) \big) + \sum_{t=2}^{T} \mathbb{E}_{q(z_{t-1}|\mathbf{x},\mathbf{u},\phi)} \big[ \mathrm{KL} \big( q_t(z_t|z_{t-1},\mathbf{x},\mathbf{u},\phi) \;\|\; p(z_t|z_{t-1},u_{t-1},\theta) \big) \big] }$

（長い…）まとめると、状態空間モデルの変分下限は次のように書くことができる。

$\displaystyle { \mathcal{L}(\mathbf{x}, \mathbf{u}; \theta,\phi) }$

$\displaystyle { \quad = \sum_{t=1}^{T} \mathbb{E}_{q(z_t|\mathbf{x},\mathbf{u},\phi)}[\log p(x_t|z_t,\theta) ] }$

$\displaystyle { \qquad - \mathrm{KL}\big( q_1(z_1|\mathbf{x},\mathbf{u},\phi) \;\|\; p(z_1) \big) }$

$\displaystyle { \qquad - \sum_{t=2}^{T} \mathbb{E}_{q(z_{t-1}|\mathbf{x},\mathbf{u},\phi)} \big[ \mathrm{KL} \big( q_t(z_t|z_{t-1},\mathbf{x},\mathbf{u},\phi) \;\|\; p(z_t|z_{t-1},u_{t-1},\theta) \big) \big] }$